Лабораторная работа №3

Условный оператор

Решение нулевого варианта

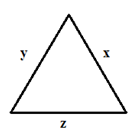
Задача. Даны действительные положительные числа x, y и z. Выяснить существует ли треугольник с длинами сторон x, y и z. Если треугольник существует, то вычислить его площадь.

Входные данные: x, y, z - три стороны треугольника.

Выходные данные: сообщение “Треугольник с такими стороны не существует” или “Треугольник с такими сторонами существует”. В последнем случае выводится площадь треугольника s.

Треугольник существует только тогда, когда сумма двух его любых сторон больше или равна третьей. Т.е. требуется сравнить длину каждого отрезка с суммой двух других.

Рис.13

 

 

Если треугольник с такими сторонами существует, то необходимо найти площадь треугольника по формуле Герона:

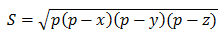 , где x,y,z — стороны треугольника, p — полупериметр, который вычисляется по формуле: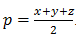 

Для того чтобы сообщения “Треугольник с такими стороны не существует” или “Треугольник с такими сторонами существует” отображались корректно, необходимо  использовать функцию setlocale(LC_ALL,"Russian") внутри функции main().

Текст программы:

#include "stdafx.h"

#define _USE_MATH_DEFINES

#include <iostream>

#include <cmath>

#include <clocale>

using namespace std;

int _tmain(int argc, _TCHAR* argv[])

{setlocale (LC_ALL,"Russian");

       float x,y,z,p,s;      bool q;

       cout <<"x="; cin >>x;

       cout <<"y="; cin >>y;

       cout <<"z="; cin >>z;

       if (x+y>=z && y+z>=x && x+z>=y) q=true; else q=false;

       if (q) {cout<<"\nТреугольник с такими сторонами существует\n";

                     p=(x+y+z)/2;

               s=sqrt(p*(p-x)*(p-y)*(p-z));

       cout<<"\nПлощадь треугольника:"<<s<<'\n';}

       else cout<<"\nТреугольника с такими сторонами не существует\n";

    system("pause");

       return 0;}

Задания для самостоятельного выполнения:

  1. Даны действительные числа x,y,z. Получить: max(x,y,z).
  2. Даны действительные числа x,y,z. Получить: max(x+y+z, xyz).
  3. Даны действительные числа x,y,z. Получить: 
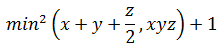
  4. Даны действительные числа a,b,c. Проверить, выполняется ли следующее неравенство a<b<c.
  5. Даны действительные числа a,b,c. Удвоить эти числа, если a≥b≥c, и заменить их абсолютными значениями, если это не так.
  6. Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения:
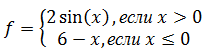
  7. Для данного целого x найти значение следующей функции f, принимающей значений целого типа:
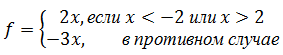
  8. Дано данного вещественного x найти значение следующей функции f, принимающей вещественные значения:
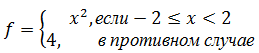
  9. Для данного вещественного x найти значения следующей функции f, принимающей вещественные значения:
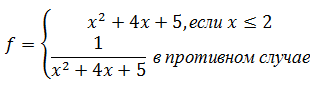
  10. Даны три целых числа. Найти количество положительных и количество отрицательных чисел в исходном наборе.
  11. Даны три действительных числа. Возвести в квадрат те их них, значения из которых неотрицательны.
  12. Даны две переменные вещественного типа:А, В . Если их значения не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения. вывести новые значения переменных А и В.
  13. Даны три переменные вещественного типа А, В, С. Если их значения упорядочены по возрастанию, то удвоить их; в противном случае заменить значений каждой переменной на противоположное. Вывести новые значения А, В, С.
  14. Даны четыре целых числа, одно из которых отлично от трех других, равных между собой. Определить порядковый номер числа, отличного от остальных.
  15. Даны координаты точки, не лежащей на координатных осях О(Х) и О(У). Определить номер координатной четверти, в которой находится данная точка.

                     

Вернуться к теории